|
周赛地址:https://leetcode-cn.com/contest/weekly-contest-228/
考虑两种最终情况,一个字符串,要想构造成“交替二进制”,一种是0开头,一种是1开头,和下标联系起来,即奇数下标放奇数偶数下标放偶数和奇数下标放偶数偶数下标放奇数。
这是两个最终状态,遍历字符串,向两种最终状态进行改变,记录改变的次数,取两个次数的最小值即可。
class Solution {
public int minOperations(String s) {
int length = s.length();
int count1 = 0, count2 = 0;
for (int i = 0; i < length; i++) {
// 奇数下标放奇数,偶数下标放偶数
if ((i & 1) == 1) {// 奇数下标
if (s.charAt(i) == '0') {
count1++;
}
} else {// 偶数下标
if (s.charAt(i) == '1') {
count1++;
}
}
// 奇数下标放偶数,偶数下标放奇数
if ((i & 1) == 1) {// 奇数下标
if (s.charAt(i) == '1') {
count2++;
}
} else {// 偶数下标
if (s.charAt(i) == '0') {
count2++;
}
}
}
return Math.min(count1, count2);
}
}
首先看懂同构字符串的定义。假设在字符串s中可以找到一个长度为n的字符相同的字符串,这里以n个'a'字符举例,那么这个字符串对同构子字符串数目的贡献为n个'a',n-1个'aa',n-2个'aaa',……,1个'aaa……a',它们的和是 。 。
于是问题转化成:将字符串s分割成若干个小字符串,每个小字符串里,只包含同一个字符,长度尽可能长,分别计算出每个小字符串对总数目的贡献度,进行求和,注意上溢出。
class Solution {
public int countHomogenous(String s) {
s += ' ';// 添加一个额外字符,否则需要对最后一段进行特判
long length = s.length(), MOD = (long) 1e9 + 7, count, result = 0, sub;// 用int会溢出
for (int i = 0; i < length; i++) {
// 从i位置向后找,直到找到一个不等于s[i]字符的位置,计算这段的贡献度
for (int j = i + 1; j < length; ) {
if (s.charAt(i) == s.charAt(j)) {
j++;
} else {
sub = j - i;
// count = (j - i + 1) * (j - i) / 2;这么写会溢出,因为int * int结果还是int,但是结果已经超过了int的上限
count = (sub + 1) * sub / 2;
if (count > MOD) {
count %= MOD;
}
result += count;
i = j - 1;
break;
}
}
}
return (int) (result % MOD);
}
}
观察数据量,maxOperstion最大可以取到1e9,所以不能真的操作这maxOperations次后,再查看结果,如果这么做了,决策正确的话,肯定会超时,因此只能将问题进行转化。
先考虑这么一个问题,有一个袋子里有n个球,进行若干次操作,让最多球的袋子里球的个数不超过y,你会不会分?肯定会吧。那么这么分配,你最少需要几步来完成呢?假设需要x步骤完成。若x>maxOperations,那么就需要增大y,从而减少x;若x≤maxOperations,那么就需要减小y,从而增大x,直到找到一个点:最多球的袋子里,球的个数是y,操作次数是x,满足x≤maxOperations,倘若y变成y-1,x随之增大,不满足x≤maxOperations了,那么,之前的y就是要求的答案。
此时,问题变成:在1~1e9的区间内,二分查找一个最小的y,使得x≤maxOperations。
class Solution {
public int minimumSize(int[] nums, int maxOperations) {
int left = 1, right = 1000000000, result = 0;
// 二分查找y(也就是这里的mid)
while (left <= right) {
// mid是当前需要检测的值
int mid = (left + right) / 2;
// 对大于mid的袋子进行拆分,每次从里面取mid个球,计算需要操作的次数,看看有没有超过maxOperations
int operation = 0;
for (int i : nums) {
if (i > mid) {
if (i % mid == 0) {
operation += i / mid - 1;
} else {
operation += i / mid;
}
}
}
if (operation <= maxOperations) {// 操作次数过少或符合要求,需要减小y
right = mid - 1;
result = mid;// 符合要求,把mid记录一下,否则需要分析取左边界还是右边界
} else {// 操作次数过多,需要增大y
left = mid + 1;
}
}
return result;
}
}
看了题解,就傻眼了,竟然是直接暴力,数据规模不大,400个顶点,时间复杂度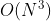 ,直接上代码吧。 ,直接上代码吧。
class Solution {
public int minTrioDegree(int n, int[][] edges) {
boolean[][] graph = new boolean[n + 1][n + 1];
int[] degree = new int[n + 1];
int min = Integer.MAX_VALUE;
for (int[] edge : edges) {
graph[edge[0]][edge[1]] = graph[edge[1]][edge[0]] = true;
degree[edge[0]]++;
degree[edge[1]]++;
}
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
for (int k = j + 1; k <= n; k++) {
// i,j,k连通,表示以i,j,k为顶点的图构成三元组
if (graph[i][j] && graph[j][k] && graph[k][i]) {
// 减去6的意思是i,j,k内部的度,i-j,j-k,k-i之间都有连线,无向图中,一条边对应两个度
min = Math.min(min, degree[i] + degree[j] + degree[k] - 6);
}
}
}
}
return min == Integer.MAX_VALUE ? -1 : min;
}
}
|