|
目录
前沿
算法基础理论
算法模型
参数分析
C++程序测试Sphere函数
总结
visual studio2017c++源代码
源文件下载地址
模拟退火法(simulated annealing algorithm,SAA)的基本思想源于物理中固体物质的退火过程与一般的组合优化问题之间相似,它把优化问题的可行解视为材料的各种状态,优化目标视为材料的能量或者熵,在优化过程中不断的“产生新解——判断——接受或舍弃”进行迭代,最终实现问题的最优化。
| 组合优化问题 | 金属物体 | | 解 | 粒子状态 | | 最优解 | 能量最低的状态 | | 设计初温 | 溶解过程 | | Metropolis抽样过程 | 等温过程 | | 控制参数的下降 | 冷却 | | 目标函数 | 能量 |
- 解决多项式复杂程度的非确定性(NP)复杂性问题;
- 克服优化过程陷入局部极小;
- 克服初值依赖性。
在对固体物质进行模拟退火处理时,通常先将它加温熔化,使其中的粒子可自由运动,然后随着温度的逐渐下降,粒子也逐渐形成了低能态的晶格。若在凝结点附近的温度下降速率足够慢,则固体物质一定会形成最低能态的基态。

固体退火过程
退火是指将固体加热到足够高的温度(熔化),使分子呈随机排列状态(熵增大、能量增大),然后逐步降温使之冷却(冷却),最后分子以低能状态排列(熵减小、能量减小),固体达到某种稳定状态。
- 加温过程——增强粒子的热运动,消除系统原先可能存在的非均匀态;
- 等温过程——对于与环境换热而温度不变的封闭系统,系统状态的自发变化总是朝自由能减少的方向进行,当自由能达到最小时,系统达到平衡态;
- 冷却过程——使粒子热运动减弱并渐趋有序,系统能量逐渐下降,从而得到低能的晶体结构。
退火过程中的统计力学
此部分主要描述了退火过程中所有状态在高温下具有相同概率以及温度降至很低时,材料倾向于进入具有最小能量的状态。
Metropolis准则——以一定概率接受新状态
(1)若在温度T,当前状态i → 新状态j
(2)若 ,则接受 j 为当前状态; ,则接受 j 为当前状态;
(3)否则,若概率 p大于[0,1)区间的随机数,则仍接受状态 j 为当前状态;若不成立,则保留状态 i 为当前状态。

在高温下,可接受与当前状态能量差较大的新状态;在低温下,只接受与当前状态能量差较小的新状态。

模拟退火法流程图
初始温度
初温越大,获得高质量解的机率越大,但花费较多的计算时间。
方法:
1)均匀抽样一组状态,以各状态目标值的方差为初温;
2)随机产生一组状态,确定两两状态间的最大目标值差,根据差值,利用一定的函数确定初温,譬如  ,其中 ,其中 为初始接受概率; 为初始接受概率;
温度更新函数
温度更新函数,即温度的下降方式,用于在外循环中修改温度值。
常用的算法温度下降函数:
1) :α越接近1温度下降越慢,且其大小可以不断变化; :α越接近1温度下降越慢,且其大小可以不断变化;
2) :其中 :其中 为起始温度,K为算法温度下降的总次数。 为起始温度,K为算法温度下降的总次数。
终止准则
外循环终止准则
- 设置终止温度的阈值;
- 设置外循环迭代次数;
- 算法搜索到的最优值连续若干步保持不变;
- 概率分析方法。
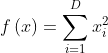
通过程序计算,用origin整理如下:

SA算法的优点:
- 质量高;
- 初值鲁棒性强;
- 简单、通用、易实现。
SA算法的缺点:
由于要求较高的初始温度、较慢的降温速率、较低的终止温度,以及各温度下足够多次的抽样,因此优化过程较长。
pch.h头文件:
// Simulated annealing.cpp : 模拟退火程序编写
//开发人员:陈帅 日期:2019.8.3-9.4 邮箱:chenshuai0614@hrbeu.edu.cn
#ifndef PCH_H
#define PCH_H
#include <iostream>
# include <fstream>
#include <iomanip>
#include <math.h>
#include <vector>
#include<random>
#include<ctime>
using namespace std;
//产生随机小数或整数
class RandomNumber {
public:
RandomNumber() {
srand(time(0)); //析构函数,在对象创建时数据成员执行初始化操作
}
int integer(int begin, int end)
{
return rand() % (end - begin + 1) + begin;
}
double decimal(double a, double b)
{
return double(rand() % 10000) / 10000 * (b - a) + a;
}
};
//定义推过过程中材料的各种固有属性
class sa
{
private:
//=====================模拟退火算法参数=====================
int T_0 ; //设置初始温度 跟跳出目前优化状态相关
int L_0 ; //设置循环次数
int T_s ; //停止准则温度为0
int K ; //停止准则2
int n_variable ; //变量数量
double alpha ; //降温系数
public:
vector<double>x_low = { -100 }; //储存变量上限值
vector<double>x_high = { 100}; //储存变量下限值
vector<double>x_i; //初始优化变量赋值
vector<double>x_new; //新状态优化变量赋值
vector<double>x_best; //最优变量
double Ene_value; //能量值
double Ene_value_new; //新状态能量值
double Ene_delta; //能量差值
double Ene_best; //最优能量值
double P_T; //P_T以一定的概率接受不好的状态
double T_k; //更新温度
void SetParameters(); //设置算法参数
void intialize(); //初始化
void metropolis(); //metropolis准则
void update_var_Ene(); //能量更新
void Optimization_iteration(); //寻优迭代
};
double function(vector<double> x); //目标函数
#endif //PCH_H
Simulated annealing.cpp主函数文件:
#include "pch.h"
#include <iostream>
RandomNumber r; //随机数
int main()
{
sa SA; //定义物体,包括材料的各种固有属性
SA.SetParameters();
SA.intialize(); //初始化
SA.Ene_value = function(SA.x_i); //计算目标测试函数
SA.Ene_best = SA.Ene_value;
//进入主要循环,按照公式依次迭代,直到满足精度要求
SA.Optimization_iteration();
}
sa_function.cpp函数文件:
#include "pch.h"
double function(vector<double> x)
{
double fx = 0;
int n = size(x);
//============================测试函数=============================
//1.Sphere函数 变量[-100,100]
for (int i = 0; i < n; i++)
{
fx = fx + pow(x[i], 2);
}
return fx;
}
void sa::SetParameters()
{
T_0 = 1500; //设置初始温度 跟跳出目前优化状态相关
L_0 = 200; //设置循环次数
T_s = 1; //停止准则温度为0
K = 400; //停止准则2
n_variable = 2; //变量个数
alpha = 0.99; //降温系数
}
//*********************************
//初始化
//*******************************
void sa::intialize()
{
extern RandomNumber r; //随机数
x_i.resize(n_variable); //定义初始优化变量的值
x_new.resize(n_variable); //定义优化变量更新值
x_best.resize(n_variable); //最优变量初始化
T_k = T_0;
for (int i = 0; i < n_variable; i++)
{
x_i[i] = r.decimal(x_low[0], x_high[0]); //给变量赋值新状态/新的可行解
}
}
//***************************
//更新新状态下的变量和最优能量值
//******************************
void sa::update_var_Ene()
{
extern RandomNumber r; //随机数
//旧状态下的函数值
for (int i = 0; i < n_variable; i++)
{
x_new[i] = r.decimal(x_low[0], x_high[0]); //给变量赋值新状态/新的可行解
}
Ene_value_new = function(x_new); //新状态下的函数值
//选优
if (Ene_value_new < Ene_best)
{
Ene_best = Ene_value_new;
x_best = x_new; //更新最优变量
x_i = x_new; //更新变量
}
}
//***************************
//metropolis准则
//******************************
void sa::metropolis( )
{
extern RandomNumber r; //随机数
Ene_delta = Ene_value_new - Ene_value; //能量(函数)差值
if (Ene_delta > 0)
{
P_T = exp(-Ene_delta / (T_0));
if (P_T > r.decimal(0, 1))
{
x_i = x_new; //更新变量
// << exp(-Ene_delta / (T_0)) << endl;
}
}
Ene_value = function(x_i);
}
void sa::Optimization_iteration()
{
clock_t startTime, endTime; //定义运行时间和结束时间
startTime = clock(); //计时开始
ofstream out("模拟退火优化结果.dat");
for (int k = 0; T_k > T_s; k++) //停止准则
{
for (int l =0; l < L_0; l++) //迭代条件
{
update_var_Ene(); //更新新状态下的变量和最优能量值
metropolis(); //metropolis准则
}//某一温度下的计算结束
T_k= pow(alpha,k) * T_0; //更新温度
//T_k = double( T_0)/k;
//T_k = double( T_0)/log(k+2);
out << fixed << setw(3) << setprecision(5) << k << fixed << setw(12) << setprecision(5) << Ene_best << endl;
}
out << "最优变量:" << endl;
for (int i = 0; i < n_variable; i++)
{
out << "x" << i << "=" << fixed << setw(12) << setprecision(5) << x_best[i] << endl;//输出最优变量
}
out << "最优值=" << fixed << setw(12) << setprecision(5) << Ene_best << endl;
endTime = clock();//计时结束
out << "run time:" << (double)(endTime - startTime) / CLOCKS_PER_SEC << "s" << endl;
out.close();
}
https://download.csdn.net/download/weixin_41788456/11828587
各位阅读文章的朋友觉得文章可以给个好评或者点赞,大家觉得有问题可以在评论区指出来或者发邮箱chenshuai0614@hrbeu.edu.cn联系我!如需要转载请附上链接,谢谢各位朋友!
(更新于2020.05.03) |