|
目录
深度前馈网络(deep feedforward network):
卷积神经网络(Convolutional Neural Network)
1、结构
1.1、输入层(input layer)
1.2、卷积层(convolutional layer)
1.3、线性整流层(Rectified Linear Units layer, ReLU layer)
1.4、池化层(pooling layer)
1.5、全连接层(fully-connected layer)
1.6、输出层(output layer)
训练神经网络
一、损失函数:
1、回归问题
2、分类问题
二、正则化(Regularization)
1、参数范数惩罚:
2、提前终止(early stoping)
3、Dropout
4、数据集增强
5、注入随机性
6、注入噪声
7、对抗训练(adversarial training)
三、激活函数(Activation Functions)
1、Sigmoid
2、tanh
3、ReLU
4、Leaky ReLU
5、Maxout
6、ELU
四、批量归一化(Batch Normalization)
1、简介
2、前向传播
3、反向传播
五、参数初始化(Weight Initialization)
1、初始化为小的标准正态分布
2、初始化为大的标准正态分布
3、Xavier 初始化
六、梯度下降(Gradient Descent)
固定学习率算法:
自适应学习率算法:
二阶近似方法:
-
深度前馈网络(deep feedforward network): -
1、前馈网络目标:是近似某个函数f(),定义了一个映射y=f(x;theta),并且学习参数theta的值,使它能够得到最佳的函数近似。 前馈(feedforward )是因为模型的输出和模型本身之间没有反馈连接, 当前馈网络被扩展成包含反馈连接时,它们被称为循环神经网络(recurrent neural network) -
卷积神经网络(Convolutional Neural Network) -
卷积神经网络是一类包含卷积计算且具有深度结构的前馈神经网络 1、结构  1.2、卷积层(convolutional layer) 卷积运算的目的是提取输入的不同特征,第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级,更多层的网络能从低级特征中迭代提取更复杂的特征。 感受野(receptive field):每个隐含单元连接的输入区域大小叫r神经元的感受野 一个输出单元的大小有以下三个量控制:depth, stride 和 zero-padding。 深度(depth) : 顾名思义,它控制输出单元的深度,也就是filter的个数,连接同一块区域的神经元个数。又名:depth column 步幅(stride):它控制在同一深度的相邻两个隐含单元,与他们相连接的输入区域的距离。如果步幅很小(比如 stride = 1)的话,相邻隐含单元的输入区域的重叠部分会很多; 步幅很大则重叠区域变少。 补零(zero-padding) : 我们可以通过在输入单元周围补零来改变输入单元整体大小,从而控制输出单元的空间大小。 用以下公式计算一个维度(宽或高)内一个输出单元里可以有几个隐藏单元:  W : 输入单元的大小(宽或高) F : 感受野(receptive field) S : 步幅(stride) P : 补零(zero-padding)的数量 K : 深度,输出单元的深度 

1.3、线性整流层(Rectified Linear Units layer, ReLU layer)
这一层神经的活性化函数(Activation function)使用线性整流(Rectified Linear Units, ReLU)f(x)=max(0,x)
1.4、池化层(pooling layer)
池化(pool)即下采样(downsamples),目的是为了减少特征图。池化层保持深度大小不变。
例如:max pooling,池化层规模为2*2, 步幅为2

1.5、全连接层(fully-connected layer)
全连接层的作用则是对提取的特征进行非线性组合以得到输出,即全连接层本身不被期望具有特征提取能力,而是试图利用现有的高阶特征完成学习目标。

1.6、输出层(output layer)
意义:损失函数用来量化拟合结果和真实结果之间的差异
1、回归问题
1.1、L1范数损失函数(最小绝对值误差)

1.2、L2范数损失函数(最小平方误差)

2、分类问题
2.1、多类支持向量机损失 Multiclass SVM Loss
SVM的损失函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值 。 。
如果正确分类得分比不正确分类得分高出 ,则损失为0,否则为:正确分类得分 - 不正确分类得分 + ,则损失为0,否则为:正确分类得分 - 不正确分类得分 + 
SVM分类器使用的是折叶损失(hinge loss),有时候又被称为最大边界损失(max-margin loss)

计算例子:

2.2、Softmax Classifier (Multinomial Logistic Regression)(softmax分类器,多分类逻辑回归)
softmax函数:
Softmax分类器使用的是交叉熵损失(corss-entropy loss)

计算例子:

意义:机器学习的一个核心问题是设计不仅在训练数据上表现好,而且能在新输入上泛化好的算法。在机器学习中,许多策略被显式地设计来减少测试误差(可能会以增大训练误差为代价)。这些策略被统称为正则化(Regularization)。
1、参数范数惩罚:

1.1、L1正则化

相比L2正则化,L1正则化会产生更稀疏(sparse)的解(此处的稀疏性指的是最优值中的一些参数为0)。由L1正则化导出的稀疏性质已经被广泛地用于特征选择(feature selection)
1.2、L2正则化

通常称为权重衰减(weight decay)
1.3、L1和L2的组合

2、提前终止(early stoping)
当训练有足够的表示能力甚至会过拟合的大模型时,训练误差会随着时间的推移逐渐降低,但验证集的误差会再次上升。
提前终止策略:在每次验证集误差下降的时候,我们储存模型参数的副本;当验证集上的误差在事先指定的循环次数内没有进一步下降时,算法就会终止。当训练算法终止时,我们返回储存的模型参数。
优点是:有效性和简单性
3、Dropout
在每次前向传播中,随机将一些单元的输出乘以0,类似把它们丢掉。丢掉的比例是一个超参数。隐藏层一般是0.5(采样率0.5),输入层一般是0.2(采样率0.8).
优点是:1、计算方便 2、不怎么限制适用的模型或训练过程,几乎在所有使用分布式表示且可以用随机梯度下降训练的模型上都表现很好。包括前馈神经网络、受限玻尔兹曼机以及循环神经网络
缺点:1、只有极少的训练样本可用时,Dropout不会很有效 2、当有其他未分类的数据可用时,无监督特征学习也比Dropout更有优势。
4、数据集增强
让机器学习模型泛化得更好的最好办法是使用更多的数据进行训练。我们可以创建人工数据并添加到训练集中。
这个方法对分类的对象识别问题很有效。我们可以对原始图片进行翻转、旋转、随机裁剪缩放,色彩抖动来获得新的图片数据。
5、注入随机性
在训练中加入一些随机性,在测试的过程中使用一些基于全局估计的正则化来抵消这个随机性。
例子:Batch Normalization
6、注入噪声
将噪声作用于输入,作为数据集增强策略。
将噪声作用于隐藏单元,例子:Dropout、Stochastic Depth、Fractional Max Pooling
将噪声作用于权重(weight),这项技术主要用于循环神经网络。例子:DropConnect
将噪声作用于输出,例子:标签平滑(label smoothing)
7、对抗训练(adversarial training)
对抗样本(adversarial example):人类观察者不会察觉原始样本和对抗样本之间的差异,但是网络会做出非常不同的预测。
对抗训练:把对抗样本当作新的训练样本加入到训练集中,原始样本加上对抗样本一起训练。
-
三、激活函数(Activation Functions)
1、Sigmoid


优点:1、数据输出范围(0,1)
2、以前比较流行,因为生物学上可以近似看作是一种神经元的饱和放电率
缺点:1、饱和的部分会出现梯度消失
2、输出不是以0为中心的对称
3、exp()指数计算耗时间
2、tanh

优点:1、数据输出范围(-1,1),以0为中心对称
缺点:1、饱和的部分会出现梯度消失
3、ReLU


优点:1、在正的区域不会饱和(不会出现梯度消失)
2、计算效率高
3、比Sigmoid/tanh收敛得更快(经验值:快6倍左右)
4、在生物学上的解释比Sigmoid更合理些
缺点:1、不是以0为中心对称
2、一些ReLU单元会“挂掉”
4、Leaky ReLU
 PReLU: PReLU: 
优点:1、拥有ReLU的所有优点
2、不会“挂掉”
缺点:1、不是以0为中心对称
5、Maxout

优点:1、非线性
2、综合了ReLU和Leaky ReLU
3、不会饱和(不会出现梯度消失),不会“挂掉”
缺点:1、参数加倍了
2、不是以0为中心对称
6、ELU

优点:1、拥有ReLU的所有优点
2、更接近以0为中心对称
3、和Leaky ReLU相比,负区域增加了对噪声的鲁棒性
缺点:1、exp()指数计算耗时间
-
四、批量归一化(Batch Normalization)
1、简介
Batch Normalization(批量归一化)在2015年提出来,论文地址。
机器学习在输入数据由均值为0,单位方差的不相关特征构成的时候往往表现得更好,但随着网络的训练,每层的weight在不断更新,导致后面layer的输入数据会发生偏移,不再具有均值为0或单位方差,而数据进入网络前,进行数据预处理解决不了这个问题。所以提出了Batch Normalization。
位置:批量归一化通常在全连接层(fully-connected layer)或卷积层(convolutional layer)之后,线性整流层(ReLU layer)之前

优点:1、允许使用更高的学习率
2、减少对参数初始化的依赖
3、具备正则化的功能,一般使用了BN,就不用使用Dropout
4、改善梯度流
2、前向传播
2.1、训练时,基于每个batch进行归一化, 和 和 是可学习参数 是可学习参数

2.2、测试时,使用固定的全局的 和 和 (训练时收集到的运行均值) (训练时收集到的运行均值)
2.3、公式:

代码例子:
if mode == "train":
sample_mean = x.mean(axis=0)
sample_var = x.var(axis=0)
sample_x = (x - sample_mean) / (np.sqrt(sample_var + eps))
out = gamma * sample_x + beta
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
elif mode == "test":
sample_x = (x - running_mean) / (np.sqrt(running_var + eps))
out = gamma * sample_x + beta
3、反向传播
公式:

代码例子:
m = x.shape[0]
dgamma = np.sum((dout * sample_x),axis=0)
dbeta = np.sum(dout,axis=0)
dsample_x = dout * gamma
dvar = np.sum(dsample_x*(x-sample_mean)*(-0.5)*np.power(sample_var+eps,-1.5), axis=0)
dmean = np.sum((dsample_x/-np.power(sample_var+eps,0.5)) + dvar*np.mean(-2*(x-sample_mean)),axis=0)
dx = dsample_x/np.power(sample_var+eps,0.5) + dvar*2*(x-sample_mean)/m + dmean/m
-
五、参数初始化(Weight Initialization)
1、初始化为小的标准正态分布

对于小网络可行,
但是对于更深的网络会有问题:因为每次乘的W都很小,会导致每层的输出越来越小,趋向于0。反向传播时,梯度也会趋向于0.
2、初始化为大的标准正态分布

大的W会导致输出过大,这样经过线性整流层(ReLU layer)时会饱和,都输出1或-1,导致梯度都为0(梯度消失)
3、Xavier 初始化

初始化效果不错,但是激活函数为ReLU时表现不好。因为ReLU每次几乎会kill掉一半的单元,这个公式每次除以的还是全部单元的方差,修改后的公式如下,可以在使用ReLU时也表现不错。

固定学习率算法:
1、批量梯度下降(Batch Gradient Descent)
BGD 每一次迭代采用整个训练集的数据来计算 cost function 对参数的梯度,所以计算起来会很慢,特别是数据量很大的时候,计算量很大,而且对内存容量也有要求(m为样本总量,n为迭代总次数):

评价:BGD对于凸函数可以收敛到全局极小值,对于非凸函数可以收敛到局部极小值
2、小批量梯度下降(Mini-Batch Gradient Descent)
和 SGD 的区别是每一次循环不是作用于每个样本,而是具有 b 个样本的批次(m为样本总量,b是每一批的样本数量)。

评价:MBGD 每一次利用一小批样本,即 b 个样本进行计算,这样它可以降低参数更新时的方差,收敛更稳定,另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。
3.、随机梯度下降(Stochastic Gradient Descent)
和BGD 的一次迭代用所有数据计算梯度相比,SGD 每次迭代时对每个样本进行梯度更新。1、先将训练数据随机打乱顺序 2、重复m次迭代,每次使用一个训练数据来计算cost fuction对参数的梯度。(m为样本总量)

评价:1、因为每次只使用一个样本进行更新,所以会造成 cost function 有严重的震荡
2、SGD的噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。所以虽然训练速度快,但是准确度下降,并不是全局最优。虽然包含一定的随机性,但是从期望上来看,它是等于正确的导数的。
梯度下降遇到的问题:局部极小值和鞍点
在这两个地方,梯度为0,会导致梯度下降算法卡在这里。一般来说鞍点更加普遍,特别是在高维空间。
解决:使用带动量的梯度下降算法可以很好地处理局部极小值和鞍点的问题

4、随机梯度下降+标准动量(SGD + Momentum)

之前的步长是梯度(dx)*学习率(learning_rate),现在的步长是速度(vx)*学习率(learning_rate)。
速度(vx)=摩擦系数(rho)*速度(vx)+梯度(dx)
加上动量的好处:1、解决了局部极小值和鞍点的问题,在这些点上依然会有速度,所以即使梯度为0,但步长不会为0
2、加上动量以后,加快了下降的速度,由此加快了学习的速度 (黑色曲线:SGD,蓝色曲线:SGD+Momentum)

5、随机梯度下降+Nesterov 动量(SGD + Nesterov Momentum)
步长比较:

Nesterov动量和标准动量之间的区别体现在梯度计算上,Nesterov动量中,梯度计算放在施加当前速度之后(下图蓝框)。因此,Nesterov动量可以解释为往标准动量方法中添加了一个校正因子。
在凸批量梯度的情况下,Nesterov动量将额外误差收敛率从O(1/k)(k步后)改进到O(1/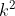 )。可惜,在随机梯度的情况下,Nesterov动量没有改进收敛率。 )。可惜,在随机梯度的情况下,Nesterov动量没有改进收敛率。


自适应学习率算法:
学习率是难以设置的超参数之一,因为它对模型的性能有显著的影响。
1、AdaGrad

随着时间增加,grad_squared会累积越来越大,由此步长会越来越小。
对于凸函数来说,在极值点周围步长会慢慢减少,这个性质帮助函数更好的收敛
对于非凸函数来说,在经过局部极值点时,可能会卡在那里。
2、RMSProp

decay_rate通常是0.9或0.99
RMSProp有点像给梯度的平方加上动量,使其不会卡在局部极值点。所以RMSProp在非凸函数上表现得更好。

3、Adam

Bias项用来避免一开始出现很大的步长
Adam有点像RMSProp和动量的结合,通常对超参数的选择相当鲁棒,适合做默认算法。

二阶近似方法:
待续。。。
|